How to Master Physics: From Basic Waves to Quantum Models (A Proven Method)

Here’s something fascinating – Quantum cryptography has been tested in Switzerland for secure electronic voting in pilot projects showcasing real-world use of quantum technology in data protection. And in 2017, Chinese physicists achieved another breakthrough by quantum teleporting information from Tibet to a satellite 1,400 kilometers above Earth.

Students who become skilled at physics learn more than abstract concepts, they understand the science that shapes our modern world. Wave functions that describe electron behavior and the quantum mechanical model that explains particle interactions connect directly to everyday technology. These same wave principles help explain how millions of transistors work together in the computer chip that powers your phone and laptop.

A solid grasp of advanced physics begins with waves and optics. The learning path moves through mechanics and statistics to conclude with quantum concepts like wave-particle duality and the uncertainty principle. These topics might seem daunting at first glance, but they follow a logical sequence that anyone can understand with proper guidance.

This piece offers a proven method to guide you through this fascinating progression from simple wave behavior to complex quantum models. You’ll build strong foundations to understand physics concepts that have transformed our view of the universe.

Start with Waves: The Foundation of Physical Systems

Waves help us understand physical systems throughout our universe. A pebble creating ripples in a pond shows how waves move energy from one place to another. These patterns are the foundations of both classical and quantum physics.

Understanding mechanical and electromagnetic waves

Physical waves fall into two basic categories that act differently but share significant characteristics. Mechanical waves need a medium to travel through and cannot exist in a vacuum. These disturbances move through matter; solid, liquid, or gas. Water ripples, sound waves in air, and seismic waves during earthquakes are common examples.

Electromagnetic waves can travel through a complete vacuum. They consist of electric and magnetic fields that move perpendicular to each other. Radio waves, microwaves, infrared light, visible light, ultraviolet light, X-rays, and gamma rays make up the electromagnetic spectrum. These waves don’t need particles to transfer energy, which explains why sunlight reaches Earth through the vacuum of space.

Both types share a vital similarity: they move energy without moving matter. The particles in a medium vibrate but stay in roughly the same spot while energy moves forward.

Key principles of waves and optics

All waves share basic properties that let us measure and predict their behavior. The wavelength (λ) measures the distance between similar parts of a wave, like crest to crest or trough to trough. Frequency (f) shows how many waves pass a point each second, while period (T) measures the time for one complete wave cycle.

These properties connect through the wave equation: v = fλ, where v shows wave velocity. This equation proves that in a medium with constant velocity, higher frequency creates shorter wavelength.

Amplitude measures the maximum displacement from equilibrium and relates to the wave’s energy. Sound waves’ amplitude changes volume, while light waves’ amplitude affects brightness.

These wave principles build the foundation to grasp more complex physics. These concepts apply to simple water waves and quantum mechanical models where particles show wave-like properties.

How wave behavior guides interference and diffraction

Waves show unique behaviors when they meet other waves or obstacles. Interference happens when waves overlap and creates patterns of improved or reduced wave effects. Two waves meeting crest-to-crest (in phase) create constructive interference with bigger amplitude. Waves meeting crest-to-trough (out of phase) create destructive interference and might cancel each other completely.

Diffraction describes waves bending around obstacles or spreading after passing through openings. This explains why you hear someone speaking from around a corner without seeing them. The effect becomes noticeable when waves meet obstacles or openings similar to their wavelength. Any object showing diffraction must be a wave.

Becoming skilled at these wave principles helps you understand advanced concepts in physics. From optics to quantum mechanics, these wave behaviors appear in surprising ways.

From Classical to Quantum: Why Physics Needed a Revolution

Physicists’ smug confidence in the early 1900s melted away as experiments showed phenomena that classical physics couldn’t explain. Between 1900 and 1927, breakthrough discoveries changed how we see matter, predictability, and knowledge itself. Scientists didn’t throw away classical mechanics completely. They took a fresh look at basic concepts like energy and momentum instead.

Limitations of classical mechanics

Classical mechanics worked great for large objects but hit a wall at the atomic level. Late 19th century physicists had Newton’s laws of motion and Maxwell’s equations. These seemed to paint a complete picture of physical reality. The universe looked orderly and predictable back then. Matter existed as particles with clear positions, while electromagnetic radiation showed up as massless waves – two separate, unrelated things.

This comfortable view of reality soon faced serious problems. Experiments contradicted the classical idea that energy could flow in any amount continuously. Classical physics also failed to explain why subatomic objects never had clear positions and momentums. Scientists had to let go of their common-sense ideas about reality.

Blackbody radiation and the ultraviolet catastrophe

Blackbody radiation emerged as one of classical physics’ first major problems. A blackbody absorbs all electromagnetic radiation that hits it, whatever the frequency or angle might be. Classical theory’s Rayleigh-Jeans law suggested something impossible: radiation intensity would grow forever as wavelength got shorter, especially in ultraviolet ranges. Scientists called this the “ultraviolet catastrophe“.

Real experiments told a different story. Radiation intensity peaked at specific wavelengths based on temperature, then dropped at shorter wavelengths. This gap between theory and reality showed classical physics couldn’t handle atomic-scale events properly.

Max Planck cracked this mystery in 1900. He said energy comes in tiny packets called “quanta” instead of flowing smoothly. His formula E = hν, with h as Planck’s constant and ν as frequency matched the entire blackbody radiation spectrum perfectly. People first saw Planck’s quantization as just clever math, but it explained things classical physics couldn’t.

The photoelectric effect and Planck’s constant

The photoelectric effect offered more proof that classical physics fell short. Light hitting a metal surface makes electrons jump out. Classical theory predicted stronger light would give electrons more kinetic energy, while higher frequencies would just increase current.

Experiments showed something completely different. Higher frequency light gave electrons more kinetic energy, while stronger light only boosted current. Below certain frequencies, no electrons escaped at all, no matter how bright the light was.

Albert Einstein built on Planck’s quantum idea in 1905. He proposed that light itself comes as energy quanta (later named photons). Each photon carries energy E = hν and gives all its energy to one electron on the metal surface. This explained why electrons shot out instantly with dim light, as long as each photon packed enough energy.

Einstein’s equation KEelectron = hν – Φ, where Φ represents the metal’s work function matched all the photoelectric effect data. His quantum approach to light won him the Nobel Prize. It also made Planck’s constant a cornerstone of physics and launched quantum mechanics.

Wave-Particle Duality and the Birth of Quantum Thinking

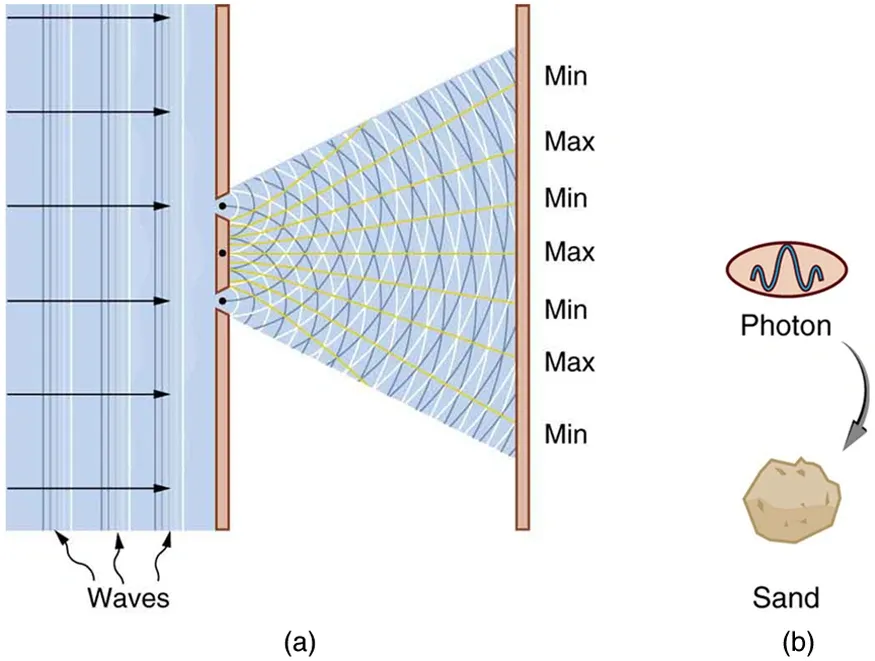
_{Image Source: Fiveable}

Richard Feynman called the double-slit experiment “the only mystery” of quantum mechanics. This experiment stands as the centerpiece of physics’ greatest transformation. A simple setup revealed matter and light’s bizarre dual nature that challenged our classical understanding of reality.

Double-slit experiment with light and electrons

Thomas Young conducted the double-slit experiment in the early 1800s and proved light’s wave nature through interference patterns. Light passing through two parallel slits creates alternating bright and dark bands on a screen. Scientists could not explain this pattern if light consisted only of particles.

The quantum strangeness became clear when scientists tested the experiment with electrons. In 1927, Davisson and Germer first proved that electrons particles with mass could act like waves. The results amazed everyone. Single electrons fired through a double-slit apparatus appeared as points on the detector screen. Many electrons passing through created an interference pattern that looked similar to waves. Each electron seemed to interfere with itself, as if it traveled through both slits at once.

Matter waves and de Broglie hypothesis

French physicist Louis de Broglie proposed his groundbreaking hypothesis in 1924. He stated that all matter has wave properties. He developed the relationship between wavelength (λ) and momentum (p) using Planck’s constant (h): λ = h/p. This equation works for everything photons, electrons, atoms, and molecules.

De Broglie’s matter wave concept explained Bohr’s quantum theory of the atom. He treated electrons as standing waves around the nucleus. This point of view made sense of why electrons occupied specific energy levels, much like a guitar string vibrates at certain frequencies.

Quantum mechanical model vs classical intuition

The quantum mechanical model clashes with our everyday understanding of reality. Classical physics shows objects following clear paths with defined positions and momenta. The quantum world defies these expectations.

Scientists discovered something unsettling when they tried to see which slit a particle passed through. The interference pattern vanished with observation. Instead, they saw the expected particle pattern. This suggests that measuring quantum objects changes how they behave.

Wave-particle duality serves as the life-blood of quantum mechanics. Nature does not follow our common-sense rules at the atomic scale. A probabilistic model takes over, where particles exist as probability waves until measured. Scientists must accept this counter-intuitive but proven reality to become skilled at physics.

Mathematical Tools: Building Blocks of Quantum Mechanics

Mathematics acts as the fundamental language that reshapes the scene of quantum mechanics from philosophical thoughts into an exact, predictable science. These mathematical tools are the foundations of mastering physics at its most fundamental level.

Complex numbers and probability amplitudes

Quantum mechanics depends on complex numbers those with the imaginary unit i (the square root of -1) unlike classical physics where real numbers are enough. Complex numbers go beyond mathematical convenience to become vital features of quantum theory. Each quantum state links to a probability amplitude a complex number whose squared magnitude gives the probability of measuring a specific outcome.

This probability connection shows that finding a particle at a particular position needs calculating |Ψ|², the square of the absolute value (or modulus) of the wave function at that point. The nature of these amplitudes explains why quantum physics deals with probabilities rather than certainties.

Operators and observables

Physical quantities like position, momentum, and energy take the form of mathematical operators in quantum mechanics rules that transform one function into another. Each observable property pairs with a specific operator. Position might multiply a function by x, while momentum involves differentiation with respect to position.

The Hamiltonian operator shows total energy and combines both kinetic and potential energy terms. Operators change quantum states, and this mathematical process mirrors how measurements affect physical systems on the ground.

Wave functions and normalization

The wave function Ψ holds complete information about a quantum system’s state. Since |Ψ|² represents probability density, a key requirement emerges: the total probability of finding a particle somewhere in space must equal 1. This mathematical constraint, called normalization, takes the form:

∫|Ψ(x)|²dx = 1

This integral, covering all possible positions, will give a physically meaningful probability.

Introduction to the Schrödinger equation

Schrödinger’s equation stands as the centerpiece of quantum mechanics and shows how wave functions change over time:

iℏ∂Ψ/∂t = ĤΨ

This equation matches Newton’s second law in classical mechanics. The term ℏ stands for the reduced Planck’s constant, and Ĥ represents the Hamiltonian operator. Physicists predict particle behavior with remarkable accuracy by solving this equation for specific systems. This mathematical framework supports the entire quantum theory.

Mastering the Models: From Square Wells to Quantum Fields

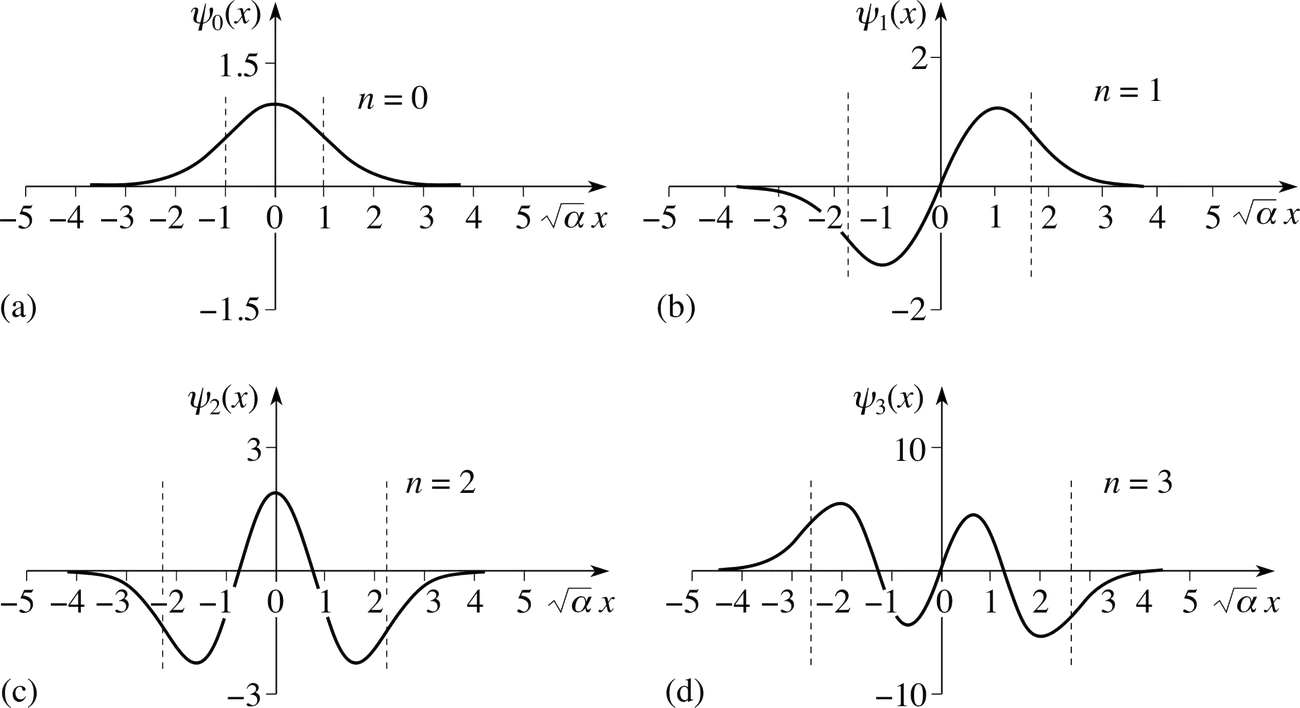
_{Image Source: www.met.reading.ac.uk}

Understanding several fundamental model systems helps you grasp physics at the quantum level. These mathematical frameworks show how particles behave in different environments. They serve as the foundation for advanced quantum applications.

Infinite and finite potential wells

The infinite potential well (particle-in-a-box) represents the simplest quantum system a particle confined to a region with impenetrable boundaries. Inside this region, particles have zero potential energy but cannot have zero total energy. The lowest allowed energy (ground state) follows E₁ = π²ℏ²/2ma², where m is mass and a is well width. Higher energies occur at En = n²E₁, creating a discrete spectrum unlike classical physics.

Particles in finite wells, where boundaries have measurable heights, show fascinating behavior. They have a nonzero probability of existing in classically forbidden regions.

Quantum harmonic oscillator

This model describes particles bound by a restoring force proportional to displacement, similar to a quantum spring. Quantum oscillators differ from classical ones in three ways: the ground state energy exceeds zero (E₀ = ℏω/2), particles exist beyond classical turning points, and particles most likely occupy the center of the well.

The oscillator’s energy levels follow En = (n + ½)ℏω, where ω represents angular frequency. This equidistant energy spacing plays a vital role in understanding molecular vibrations and phonons in solids.

Tunneling and the uncertainty principle

Quantum tunneling shows particles penetrating energy barriers they classically couldn’t overcome. The barrier’s width, height, and particle mass influence this phenomenon. Electrons can tunnel through barriers approximately 1-3 nm thick.

Heisenberg’s uncertainty principle directly leads to this effect. When position becomes precisely defined, it creates momentum uncertainty. Tunneling explains alpha decay in radioactive nuclei and makes technologies like flash memory and scanning tunneling microscopes possible.

Hydrogen atom and angular momentum

The hydrogen atom, with its single electron orbiting a proton, stands as quantum mechanics’ greatest achievement. Three quantum numbers control the electron’s behavior: principal (n) determines energy, angular momentum (l) determines orbital shape, and magnetic (m) determines spatial orientation.

Angular momentum follows strict quantization rules, with magnitude L = √(l(l+1))ℏ. This quantization explains why electrons occupy specific energy levels and show distinct orbital shapes like spherical s-orbitals or dumbbell-shaped p-orbitals.

Introduction to quantum computing

Quantum computers employ quantum mechanical effects like superposition and quantum interference. These machines solve certain problems faster than classical computers. Quantum bits (qubits) differ from classical bits because they exist in multiple states simultaneously.

A quantum computer needs five essential features: scalability, initializability, resilience, universality, and reliability known as the DiVincenzo criteria. Modern quantum computers use anywhere from a few to several tens of qubits. Their applications range from optimization problems to molecular simulation and potentially cryptography.

Conclusion

The trip from simple waves to quantum models shows a captivating progression through physics that mirrors how we’ve come to understand the universe. You’ve seen how waves act as the building blocks that help us grasp more complex physical phenomena.

Physics builds upon itself in remarkable ways. Wave principles form the foundations to understand interference and diffraction, which helps explain quantum behavior. Classical mechanics showed its limits, and this led to the quantum revolution that changed how we view reality at the subatomic level.

Wave-particle duality ranks as one of the most profound concepts in modern physics. This mind-bending principle defies common sense yet gives accurate predictions about matter’s behavior at quantum scales. You can tap into a deeper understanding of everything from electron behavior to light properties once you grasp this concept.

Mathematical tools provide the precision needed to move beyond philosophical interpretations into practical applications. Your comfort with wave functions, complex numbers, and operators will help turn abstract quantum concepts into calculable predictions about physical systems.

The rise through quantum models from simple potential wells to the hydrogen atom—shows how physicists build understanding through more sophisticated frameworks. Each model reveals fresh insights and keeps its connection to earlier fundamental principles.

Quantum mechanics might seem abstract, but its applications are everywhere in your daily life. The transistors in your electronic devices, LED lights in your home, and emerging technologies like quantum computing depend on these principles. Your mastery of physics connects you to both theoretical knowledge and practical breakthroughs that shape our world.

Note that physics mastery follows a logical path. You should start with waves, build through classical mechanics, welcome quantum thinking, and use mathematical tools to understand complex models. These concepts might seem tough at first, but they follow a clear path that anyone can learn with the right approach and steady practice.