What Top Math Students Know About Rational Expressions That You Don’t (Game-Changing)
SAT® Math questions often hide their solutions inside awkward radicals or bulky fractions. The solutions to math problems boil down to one vital skill: manipulating rational expressions.
Rational expressions are simply fractions where the numerator and denominator are polynomials. Some students excel at them while others find them challenging. The secret lies in two basic principles. You can’t divide by zero in these expressions. You need to know when factoring makes sense.
The SAT includes rational expressions with quadratic expressions and higher-order polynomials. Students who become skilled at factoring gain a clear advantage. Adding and subtracting rational algebraic expressions helps you tackle complex problems with confidence.
The best students go beyond memorizing formulas. They grasp the proportional reasoning behind rational expressions. They can spot the difference between linear and exponential functions quickly. These students know how to rewrite rational and radical expressions. This helps them avoid algebra traps and score more points on tests.
This piece reveals the strategies that math champions use to simplify, manipulate, and solve rational expressions. These techniques could be exactly what you need to complete your mathematical toolkit.
How Rational Expressions Work
Rational expressions are the foundations of many advanced mathematical concepts. Regular fractions contain only numbers, but rational expressions include polynomials in both numerator and denominator. These expressions help us discover the full potential of problem-solving in algebra and beyond.
What makes an expression ‘rational’
A rational expression works like a fraction with polynomials above and below the fraction line. To cite an instance, expressions like $frac{x+5}{x^2-4x+4}$ and $frac{x(x+1)(2x-3)}{x-6}$ qualify as rational because they use polynomial components throughout.
The domain stands as a vital aspect of rational expressions. Division by zero is impossible, so we must exclude any value that zeroes out the denominator. The expression $frac{x}{x+2}$ shows this clearly – we can’t use “x = -2” because it would make the denominator zero. We call these excluded values restrictions.
Why factoring is the key to simplification
Factoring lies at the heart of manipulating rational expressions. The simplification process requires you to:
- Factor both the numerator and denominator completely
- Identify and cancel common factors
- Write the remaining terms in simplified form
- Note any restricted values
The right factoring lets you cancel common factors, not just common terms. This significant difference matters you can only cancel factors that multiply the entire expression.
Look at $frac{x^2-9}{x-3}$ as an example. Factoring gives $frac{(x-3)(x+3)}{(x-3)}$, which becomes $(x+3)$ when $x neq 3$. This solution showcases proportional reasoning at its best.
Common mistakes with variables in denominators
Students often make mistakes by trying to “cancel” terms instead of factors. They might incorrectly simplify $frac{x^2+x}{x^2-1}$ to $frac{x+1}{x-1}$ by crossing out the $x^2$ terms. This method breaks the order of operations.
There’s another reason students struggle – they divide equations by variables without checking if those variables equal zero. You must track domain restrictions during simplification, even after canceling terms. A canceled factor affects domain restrictions because the original expression had no value at that point.
Note that adding and subtracting rational algebraic expressions differs from working with linear vs exponential functions. You need common denominators before combining terms a difference that top students grasp naturally.
Mastering the Four Core Operations
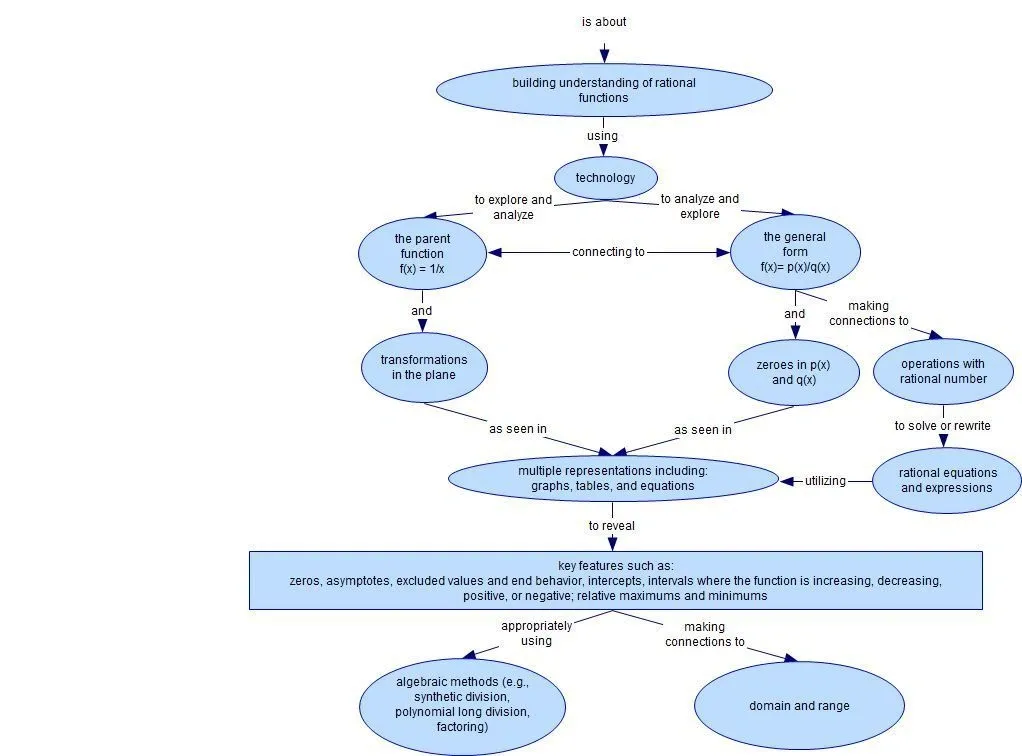
Image Source: Wayne RESA
Your success with complex algebraic problems depends on how well you handle operations with rational expressions. A solid grasp of these expressions and the four basic operations will give you practical tools to solve equations.
Simplifying before you start
The first thing you should do is simplify each rational expression before any operation. This key step involves:
- Factoring the numerator and denominator completely
- Canceling common factors (not terms)
- Noting domain restrictions where denominators equal zero
Note that canceled factors still contribute to domain restrictions since the original expression was undefined at those values. So, proper simplification helps prevent algebraic errors and makes calculations easier.
Multiplying and dividing rational expressions
Multiplying rational expressions is straightforward: multiply numerators together and multiply denominators together. In spite of that, you need to factor first to spot cancellable terms.
When dividing, you can convert to multiplication by using the reciprocal of the divisor (second fraction). The expression $frac{a}{b} div frac{c}{d}$ becomes $frac{a}{b} cdot frac{d}{c} = frac{ad}{bc}$. This transformation makes division problems easier to handle, just like in proportional reasoning.
Addition and subtraction of rational algebraic expressions
You need common denominators when adding or subtracting rational expressions. Your mathematics in action solution won’t work without this step. Adding numerators while keeping unlike denominators breaks algebraic principles.
Using least common denominators effectively
Here’s how to find the least common denominator (LCD):
- Factor each denominator completely
- List all different factors that appear in any denominator
- For repeated factors, use the highest power that appears in any denominator
- Multiply these factors together to form the LCD
Next, multiply each fraction by the appropriate form of 1 to create equivalent expressions with the LCD. You can then add or subtract the numerators while keeping the common denominator.
Want to ace your math exams? Get customized help with algebraic expressions, functions, and proportional reasoning.
Rational expressions need special attention to domain restrictions during all operations, unlike linear vs exponential functions. This detail sets top students apart from their classmates.
Rewriting Rational Expressions Like a Pro
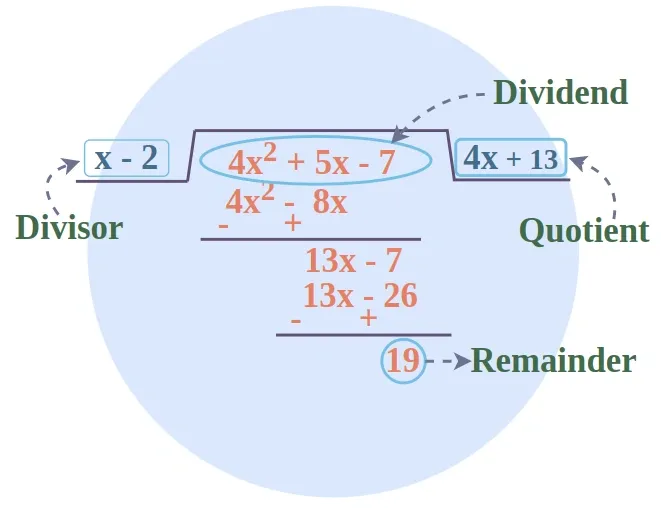
Image Source: GeeksforGeeks
The best mathematicians can do more than simple operations – they excel at completely rewriting rational expressions. This skill helps them revolutionize complex fractions into simpler forms that showcase elegant mathematics in action.
How to express as quotient and remainder
A polynomial divided by another polynomial gives a result that can be expressed as a quotient plus a remainder over the divisor. The formula looks like this: A = BQ + R, where:
- A is the dividend (numerator)
- B is the divisor (denominator)
- Q is the quotient
- R is the remainder (with degree less than B)
Let’s look at an example: (x²-3x-10)÷(x+2) can be written as (x-5) + (0)/(x+2).
Polynomial long division explained
The polynomial long division method follows the same pattern as regular arithmetic but applies to variable expressions. Here’s the process:
- Arrange both polynomials in descending order
- Divide the first term of the numerator by the first term of the denominator
- Multiply the result by the whole denominator
- Subtract this product from the numerator
- Repeat with the remainder until its degree is less than the divisor’s
When to use grouping vs. division
Polynomial long division works best with polynomials of degree 1 or higher. Synthetic division offers a quicker way with linear divisors. More importantly, factoring and grouping prove faster than division if you just need to simplify an expression rather than find a quotient plus remainder.
Whatever approach you choose, remember to identify domain restrictions where denominators equal zero.
Avoiding Pitfalls and Domain Errors
The best students can still make critical errors with rational expressions if they don’t watch out for domain restrictions. These pitfalls can revolutionize basic problem-solving into impressive mathematical solutions.
How to identify domain restrictions
Values that make denominators equal to zero create domain restrictions. Here’s how to find these values:
- Set the denominator equal to zero
- Solve for all variable values
- Exclude these values from your domain
Note that only denominators matter for domain restrictions—the numerator doesn’t affect them. Take $frac{x+3}{x^2+2x-15}$ as an example. The denominator factors to $(x+5)(x-3)$, so restrict $x neq -5$ and $x neq 3$.
Why canceled terms still matter
Original domain restrictions must stay in place after you simplify expressions. The expression $frac{(x-3)(x+3)}{(x-3)}$ simplifies to $(x+3)$, but $x neq 3$ still applies. You might include undefined values from the original expression if you ignore this.
Factoring negatives and hidden traps
Students often mix up canceling terms versus factors. You should only cancel factors that multiply entire expressions. It also helps to factor negative signs correctly: $-x+3$ becomes $-(x-3)$.
Want to excel in your math exams? We offer tailored help with algebraic expressions, functions, and proportional reasoning.
Proportional reasoning with rational algebraic expressions needs more than just adding and subtracting. The sort of thing I love about good students is how they verify answers by substituting values especially after cancellation. This approach separates average students from exceptional ones.
Conclusion
Top math students stand out from their peers without doubt because they become skilled at rational expressions. Throughout this trip, you’ve found that these expressions are just fractions with polynomials, but they need careful attention to domain restrictions and factoring techniques.
Understanding a basic principle helps you spot domain restrictions correctly – division by zero is impossible. It also saves you from common algebraic traps when you factor both numerator and denominator completely before any operation.
The four core operations simplification, multiplication, division, addition, and subtraction each need specific approaches. Multiplication and division follow straightforward processes. Students often overlook that addition and subtraction just need common denominators.
The sort of thing I love about A students is how they track canceled terms for domain restrictions. You should track all restrictions as you calculate to avoid critical errors that could cost exam points.
Knowing how to rewrite rational expressions as quotients plus remainders creates powerful problem-solving strategies for complex SAT questions. This skill combines with polynomial long division techniques to give you flexibility with difficult problems.
These game-changing strategies now give you the mathematical toolkit to handle rational expressions with confidence. Keep practicing these techniques, watch for domain restriction pitfalls, and you’ll soon tackle these problems as easily as top math students do.



